Ans: Choose the z-scores that divide the standard normal curve into 9 + 1 = 10 equal areas:
-1.28 -0.84 -0.52 -0.25 0.00 0.25 0.52 0.84 1.28
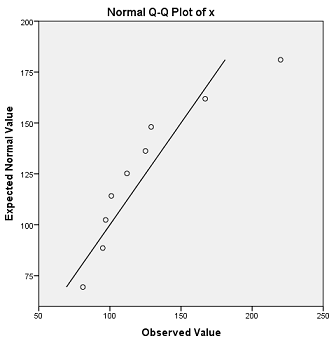
81 95 97 101 112 125 129 167 220
| a | b | c | d | e |
|---|---|---|---|---|
| 1.64 | 0.23 | 2.09 | -0.63 | 0.37 |
| -0.72 | -0.95 | 1.37 | 4.30 | 0.81 |
| Target Variable: | Numeric Expression: |
|---|---|
| Ansa | CDF.NORMAL(a, 0, 1) |
| Ansb | CDF.NORMAL(c, 0, 1) - CDF.NORMAL(b, 0, 1) |
| Ansd | CDF.NORMAL(d, 0, 1) |
| Anse | IDF.NORMAL(e, 0, 1) |

| Target Variable: | Label: | Numeric Expression: |
|---|---|---|
| Height | Height in Meters | (HeightInFeet + HeightInInch / 12.0) * 0.3048 |
| Weight | Weight in Kilos | WeightInLbs * 0.453592 |