To Notes

IT 403 -- Sept 21, 2016

Review Exercises

1. What is a z-score?
   Ans: A z-score for individual observations is computed as z = (x - x) / SD.  It tells you how many
2. standard deviations the observation is away from the mean. The z-score can also be computed for the sample mean:
   z = (x - μ) / SD_ave. If you knew the population mean μ this z would tell you how many standard errors the sample mean was from the population mean. However, μ usually unknown, so this z can be used to obtain a confidence interval for μ.
   The z for individual observations is used to look up areas under the standard normal curve.
3. When computing areas under a histogram with rectangles or under a normal curve, why do all these intervals give the same area?
   [100, 200], (100, 200], [100, 200), (100, 200).
   Ans: Because the percent of observations at a specific point is zero, it doesn't matter if we include or exclude the endpoints of the interval.
4. Approximately, what percentage of observations are in the interval [140, 450) for this histogram?
   

   0.5 +
       |
   0.4 +       +--------+
       |       |        |
   0.3 +       |        |
       |       |        |
   0.2 + +-----+        |
       | |     |        |
   0.1 + |     |        +-----------+
       | |     |        |           |
   0.0 + +-----+-----+--+--+-----+--+--+
        100   200   300   400   500   600
   

   Recall that the percent of observations in each interval is the area of the rectangle over that interval, which is computed as
        area = base * height.
        area [140, 450] = area[140, 200] + area[200, 350] + area[350, 550].
   area[200, 350] is the entire rectangle so the percent of observations in this rectangle is
   area = base * height = (350 - 200) * 0.4 = 150 * 0.4 = 60%.
   However, the interval [140, 200] only uses part of the rectangle over [100, 200]. We need to set up an equation to compute the proportion of the rectangle area over [140, 200]:
        area = base * height = (200 - 140) * 0.2 = 30%.
   The area of the third rectangle over the interval [350, 450] is
        area = base * height = (450 - 350) * 0.1 = 10%.
   The total area over [140, 450] is 12 + 60 + 10 = 82%.
   
5. What is the label for the vertical axis of the histogram in Problem 2?
   Ans: Percent per horizontal unit. The label for the horizontal axis is horizontal unit.
6. What does it mean to say that the normal distribution is ubiquitous in statistics? Ans: It means to say that the normal distribution shows up everywhere.
7. What is the ideal measurement model?
   Ans: It says that
   actual measurement = true measurement + random error
   The true measurement could be a prototype weight that does not change.  Or in the case of measuring potatos, the true measurement could be the "ideal potato" that nature is trying to produce. The random errors for the potatos are just random variations to do genetics and the environment in which the potato grows.
8. What are the official definitions of the meter, second, and kilogram?
   Ans: See the Ideal Measurement Model document.

The Cardboard Histogram

• In class last week we looked at a cardboard histogram.
• Here a rendering of it using typewriter graphics:
  

  3.0 +                 +-------+
      |                 |       |
  2.5 +                 |       |
      |                 |       |
  2.0 +                 |       |
      |                 |       |
  1.5 +         +-------+       +-------+
      |         |       |       |       |
  1.0 + +-------+       |       |       |
      | |       |       |       |       |
  0.5 + |       |       |       |       |
      | |       |       |       |       |
  0.0 + +-------+-------+-------+-------+
        0       1       2       3       4
  

• The mean of the histogram is the point on the horizontal axis where it balances over a pencil, which is at 2.1154. This is also the computed value.
• The median of the histogram is the point on the horizontal axis where, if you cut it in two pieces, each piece would weigh the same. The median is at 2.25.

Biased vs. Unbiased; Heteroscedastic vs. Homoscedastic for Graphs

• The following scatterplots are plots of x_i (measurement) vs. i (observation number) with the sample mean marked with a red horizontal line. The measurement is plotted on the vertical axis; the observation number is plotted on the horizontal axis. What does each plot tell you? Describe each plot using these terms:
  
  • Unbiased   The average of the observations in every thin vertical strip is the same all the way across the scatterplot.
  • Biased   The average of the observations changes, depending on which thin vertical strip you pick.
  • Homoscedastic   The variation (SD+) of the observations is the same in every thin vertical strip all the way across the scatterplot.
  • Heteroscedastic   The variation (SD+) of the observations in a thin vertical strip changes, depending on which vertical strip you pick.
     
    
     
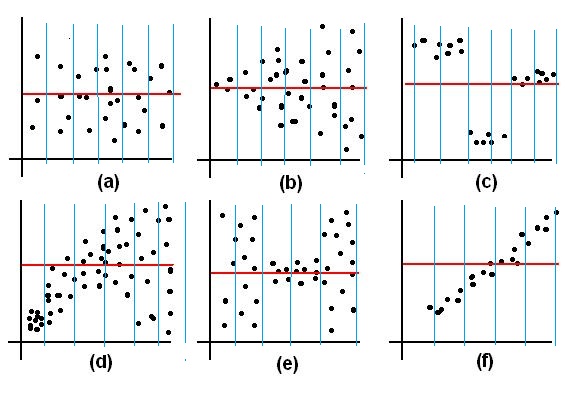
    Ans: (a) unbiased and homoscedastic, (b) unbiased and heteroscedastic, (c) biased and homoscedastic, (d) biased and heteroscedastic, (e) unbiased and heteroscedastic, (f) biased and homoscedastic.

  The Normal Distribution

  Practice Problems

  1. Work problems from the Practice Problems on the Area under the Normal Curve.

  The Standard Error of the Average

  Normal Plots

  • This section will be discussed next week on Sept 28.
  • Normal plots can be used to determine if a dataset is approximately normal, or how a dataset deviates from normality.