To Notes

IT 224 -- May 6, 2024

Review Exercises

1. What does the correlation tell you about the relationship between two data vectors x and y?
   Answer: the correlation of x and y tells you the amount of linear association between x and y.
2. Compute the correlation of x and y by hand:
   

   Obs:	1	2	3	4	5
   x:	1	2	3	4	5
   y:	1	3	2	5	4

   
   Verify your answer using R.
   Answer:
   x = (1 + 2 + 3 + 4 + 5) / 5 = 3,
   x = (1 + 3 + 2 + 5 + 4) / 5 = 3,
   SD_x = √((1-3)² + (2-3)² + (3-3)² + (4-3)² + (5-3)²) / 5) = √2
   SD_y = √((1-3)² + (3-3)² + (2-3)² + (5-3)² + (4-3)²) / 5) = √2
   Now compute the z-scores for both x and y:
   z_xi = (x_i - x) / SD_x  and z_yi = (y_i - y) / SD_y for i = 1, ... , n.
   Then the correlation is the average of the products of the z-scores:
     x_i     y_i           z_xi         z_yi        z_xi*z_yi
   -----+-----+---------+---------+-----------
      1      1    -2/√(2)   -2/√(2)   +4/2 = 2
      2      3    -1/√(2)       0            0   = 0
      3       2       0         -1/√(2)       0   = 0
      4      5    +1/√(2) +2/√(2)   +2/2 = 1
      5      4    +2/√(2) +1/√(2)   +2/2 = 1  
   The average of the products is (2 + 0 + 0 + 1 + 1) / 5 = 0.8.
   Verify your calculation with R:
   

   > x <- 1:5
   [1] 1 2 3 4 5
   > y <- c(1, 3, 2, 5, 4)
   [1] 1 3 2 5 4
   > cor(x, y)
   [1] 0.8 
   

3. In the Correlation document, look at the scatterplots of bivariate datasets with various correlations.
4. Estimate the correlation r in these situations. The correct answer is marked with *:
   
   1. Height of father, height of son.
      i. -0.30    ii. 0.05    *iii. 0.70    iv. 0.99
   2. IQ of husband, IQ of wife.
      i. -0.70    ii. 0.00    *iii. 0.60    iv. 1.00
   3. Height of husband, height of wife if men always married women that were exactly 6 inches shorter.
      i. -0.60    ii. 0.60    iii. 0.99    *iv. 1.00
   4. Weight of husband, weight of wife if men always married women that weighed 70% of their weight.
      i. 0.00    ii. 0.50    iii. 0.70    (iv. 1.00
5. Match the correlation to the dataset:
   
   1. GPA in freshman year, GPA in sophomore year.  Answer: 0.70
   2. GPA in freshman year, GPA in senior year.  Answer: 0.30
   3. Length and weight of 2 by 4 boards.  Answer: 0.99
   -0.50   0.005   0.30   0.70   0.99
6. What would happen to the correlation r if
   
   1. x were replaced by x + 10.
   2. y were replaced by 2 * y + 8.
   3. x and y were interchanged.
   Answer: in all three cases, the correlation would remain the same.
7. How large must r be to be considered meaningful?
   Answer: See the table in the Correlation document.
8. Why is the computed value of r the same whether the SD or the SD+ is used for the x and y standard deviations?
9. Use R to compute the pairwise correlations of the variables in the Nielsen Dataset. The rows of this dataset are the ratings for various television shows. Interpret the correlations.

Linear Correlation Cautions

• Look at Cautions section of the Linear Correlation document.

Linear Regression

• With the Bears Roster 2024 Dataset, use R to:
  
  1. Compute the height in meters and the weight in kilos of the Bears players. The conversion rates are 0.3048 meters per foot and 0.4536 kilos per pound.
  2. Use SPSS to create a scatter plot of weight (y-axis) vs. height (x-axis).
  3. Find the simple linear regression equation for predicting weight in kilos from height in meters.
  4. Create the residual plot, which is the residuals (y-axis) vs. the predicted values (x-axis).
  5. Create the normal plot of the residuals.

Project 3

• Look at the project description for Project 3 .

The Regression Fallacy

• During their flight training, Air Force pilots make two practice landings with their instructor. The pilots that make a good first landing tend to do worse on the second landing; the pilots that make a poor first landing do better on the second landing. Conclusion: criticism helps the pilots, whereas praise hurts them. Policy change: the supervisor of the flight instructors tells them to criticize all landings, good or bad. Is this policy change warrented?
• In fact, the criticism is not warrented. This is an example of the regression fallacy.
• Look at this graph of pre-test and post-test scores marked by the dots:
  
  
  
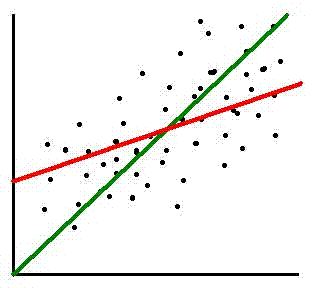
  The green line indicates where the dots would be if the pre and post scores were the same. The red line is the regression line, which shows where the pre-test score and its associated predicted post-test score would lie. As in the previous example of the Air Force pilots, a student with a high pre-test score is predicted to do worse on the post-test; a student with a low pre-test score is predicted to do better on the post-test.
• Practice Problem: Collect the following data for adult men: the subject's height, the height of the subject's father.
  
  1. Would you expect a person with a very tall father to be shorter or taller than his father?
     Answer: A very tall person is expected to be shorter than his father.
  2. Would you expect a person with a very short father to be shorter or taller than his father?
     Answer: A very short person is expected to be taller than his father.

Additional Regression Problem

• Root Mean Square Error
• A law school finds this relationship between LSAT scores (independent variable x) and first-year scores (dependent variable y). The data are bivariate normal. Here are the summary variables:
  x = 162    SD_x = 6
  y = 68    SD_y = 10
  r = 0.6
  
  1. About what percentage of the students have first-year scores over 75? Because the data are bivariate normal, the first-year scores are normally distributed, so you can use the normal table.
  2. Of those students who scored 165 on the LSAT, about what percentage have first-year scores over 75? Visualize these scores as lying in a thin vertical rectangle centered at LSAT = 165.