To Lecture Notes

CSC 423 -- 7/17/17

Course Documents

• Announcements, Professor Information, Lecture Notes, Documents, Exam Info, Projects, Syllabus, Submit Homework

Collect Micrometer Paper Thickness Measurements

• Use the instructor's micrometer to measure the thicknesses of the two sheets of paper (Blue and White) that the instructor will give you.
   
  
   
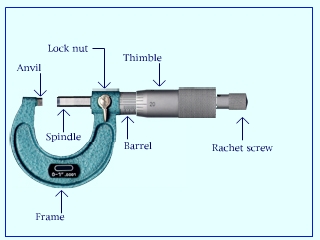
• This micrometer measures thicknesses to the nearest thousandth of a millimeter (nearest micrometer = 10^-6 m).
   
• Before you make each measurement,
   
  
  make sure that the units are set to mm, not to inches (use the mm/in button to change units if necessary),
   
  close the distance between the spindle and the anvil until they are almost touching,
   
  tighten the spindle with the ratchet screw, so that the spindle and anvil touch the sheet of paper being measured,
   
  zero out the distance on the digital display (ON/OFF 0 Button).
  
  
• When you measure each paper thickness, use the ratchet screw to obtain an accurate reading.
   
• Write your name and measured thickness in mm on each sheet of paper.
   
• These paper thickness measurements will go into a dataset that you will analyze for Project 1.

Course Topics

• Major Themes
   
  
  Regression Modeling    Statistical Software    Diagnostic Plots
  
  
• Math Prerequisites
   
  
  IT 403 or another first statistics course
  College Algebra  (We will use a little Calculus but it is not a course prereq.)
  
  
• Review of topics from IT403
   
  
  Mean  Median  Standard Deviation  Histogram  Boxplot  Normal Plot
  Scatterplot  Linear Correlation  Simple Linear Regression
  
  
• Tests of Hypothesis
   
  
  z-test  t-test  Paired-sample tests  Independent two-sample tests
  t-tests and F-tests for regression
  
  
• Simple and Multiple Linear Regression Models
   
  
  1. Horizontal Line Regression:
      
     
     y_i = μ + ε_i
      
     
  2. Regression through the Origin:
      
     
     y_i = a x_i + ε_i
      
     
  3. Simple Linear Regression:
      
     
     y_i = a + b x_i + ε_i
      
     
  4. Simple Linear Regression with log-log Transform:
      
     
     log y_i = a + b log x_i + ε_i
      
     
  5. Quadratic Regression:
      
     
     y_i = a + b x_i + c x_i² + ε_i
      
     
  6. Linear Regression, Two Independent Variables:
      
     
     y_i = a + b x_1i + c x_2i + ε_i
      
     
  7. Full Quadratic Regression, Two Independent Variables:
      
     
     y_i = a + b x_1i +  c x_2i + d x_1i² + e x_1i x_2i + f x_2i² + ε_i
      
     
  8. Matrix Form of Linear Regression Model:
      
     
     Y = Xβ + ε
     
  
  
• Regression Diagnostics
   
  
  Residual Analysis  Influence Points  Model Selection
  
  
• Analysis of Variance (ANOVA)
   
  
  Categorical Independent Variables (also called Dummy Variables)
  
  
• Logistic and Poisson Regression
   
  
  Categorical Dependent Variable

1. Give examples of continuous variables and categorical variables.
   Ans: A continuous variable can take on any value in a range (subject to roundoff error). Examples are height, stock price, price, voltage, IQ, or paper thickness.
    
   A categorical variable (also called a nominal or discrete variable) is often not a number. A categorical variable can only take on a small number of discrete values. Examples of categorical variables are gender, employment status, dog breed, country of origin.
    
   A third type of variable is an ordinal variable, which is a compromise between continuous and categorical. They can be ordered but are not continuous. For example, year in school (freshman, sophomore, junior, senior), military rank, letter grade for a course.
    
2. Explain the difference between a population and a sample.
   Ans: A population is the entire set of entities from which inferences are to be drawn. Examples of populations are adult women in the U.S., insurance companies in California, heights of fifth grade boys in California, SAS scores in Illinois, lifespans of Golden Retriever dogs, fish in Lake Michigan. A sample is a small subset of the population and can be used to perform a statistical test. For valid statistical inferences, the sample must be a simple random sample, which means that every entity in the population is equally likely to be included in the random sample.
    
   With the advent of big data, the distinction between a population and a sample is blurred; presently it is not uncommon for a company to collect data for an entire population (for example the customers that shop at Walmart). However, even if data for an entire population is collected, it is still common to extract a random sample from this data when studying some aspect of the entire population would be to time consuming or costly.
    
3. What is the name of each of these Greek letters? What do they represent in statistics?
    
   
   α    β    ε    μ    ρ    σ    θ    χ
   
   Ans:
   α: alpha, is the size or type 1 error of a statistical test (the probability of rejecting the null hypothesis when it is true). The most commonly used value for α is 0.05.
   β: beta, represents parameters of a regression equation.
   ε: epsilon, represents the random errors or residuals in a regression model.
   μ: mu, is the population mean. If the normal distribution is used, μ is the center of the normal density.
   ρ: rho, is the population correlation.
   σ: sigma, is the population standard deviation. σ² is the population variance.
   θ: theta, is an unspecified parameter in a probability density. Used for theoretical discussions and definitions.
   χ: chi, denotes the χ² (chi-squared) distribution.
   
   
4. What is a random variable?
   Ans: The formal definition of a random variable X is a function from the sample space Ω into the set of real numbers:
    
   
   X: Ω → R
   
   I prefer a more informal definition: a random variable is a process for choosing a random number.
    
5. Rewrite the expression x₁ + x₂ + ... + x_n using summation notation.
   Ans: Σ_i=1ⁿ x_i
    
6. Write the definitions of the sample mean x and the sample variance s_x² in summation notation.
   Ans: (1/n) Σ_i=1ⁿ x_i   and [(1/(n-1)] Σ_i=1ⁿ (x_i - x)²
   Notes: in the definition of s², the sum of squared deviations is divided by n-1 instead of n so that the sample variance s² is an unbiased estimator of the population variance σ²:
    
   
   E(s²) = σ²
   
    
7. Find the calculus derivative of each of these expressions:
    
   
   7x²     4x     19     4(3 - 5x)²
   
   Ans: Use the formulas (d/dx)(xⁿ) = n x^n-1 and (d/dx)(cy) = c (d/dx)(y).
   (d/dx)(7x²) = 7(d/dx)(x²) = 7(2x¹) = 14x.
   (d/dx)(4x) = 4(d/dx)(x¹ = 4(1x⁰) = 4.
   (d/dx)(19) = 19(d/dx)(x⁰) = 19(0x^-1) = 0.
   To compute the last derivative, we need the chain rule: dy/dx = (dy/du)(du/dx).
   Let y = 4(3 - 5x)² and u = 3 - 5x.
   (d/dx)(4(3 - 5x)²) = (dy/du)(du/dx) = (d/du)(4u²) (d/dx)(3 - 5x) = 8u(-5) = 8(3 - 5x)(-5) = -40(3 - 5x)
    
8. (Needed for Project 4) Compute the partial derivatives ∂y/∂x₁ and ∂y/∂x₂ for this expression:
    
   
   y = 3x₁² + 5x₁x₂ - x₂² + 7x₁ + 8x₂ + 35
   
   Ans: To compute the partial derivative ∂y/∂x₁, x₁ is the variable and x₂ is treated as a constant.
   ∂y/∂x₁ = 3(2x₁) + 5(1x₂) + 7(1) + 8(0) + 0 = 6x₁ + 5x₂ + 7
   ∂y/∂x₂ = 5(2x₁) + (-1)(1x₂) + 7(0) + 8(1) + 0 = 5x₁ - x₂ + 8
    
9. Sketch the graphs of these functions:
    
   
   y = x²      y = √x      y = e^x    y = ln x     
   
   Here are these graphs drawn by R.
    
10. Define these terms:
     
    
    Discrete Random Variable  Continuous Random Variable  Continuous Probability Density  Normal Distribution
    
    
Ans:
Discrete Random Variable: A random variable that can take on only a finite set of numeric values.
Continuous Random Variable: A random variable that can take on any value in an interval, possibly infinite like this: (-∞, ∞).
Continuous Probability Density: A positive function that is used to obtain probabilities for continuous random variables. To find P(a ≤ x ≤ b) compute the area between a and b under the probability density. If the function for the probability density is integrable, use calculus integration to find the area under the curve.  If this function is not integrable, statistical tables or software such as SAS or R is needed to compute this area.  See the Random Variable Properties and Technical Details for more explanation.
Normal Distribution: The well known bell-shaped curve. It has the probability density
φ(x) = (1 / √2π) exp((x - μ)²/(2σ²))
 
11. What is the Central Limit Theorem (CLT) and why is it important in statistics?
    Ans: The CLT states that even if n independent observations from a population do not have a normal distribution, the sample mean of the observations is approximately normally distributed if n is large. Usually we consider n to be large if n > 30, but this depends on the original distribution. If the observations are Bernoulli, with p close to 0 or 1, then n must be substantially larger than 30 for the CLT to apply.

• The standard normal density is the normal density with μ = 0 and σ = 1. Here is a graph of the standard normal density, plotted with this R script:
  

  x = seq(-4, 4, 0.01)
  y = dnorm(x)
  plot(x, y, type="l")
  

• To specify that z has a standard normal density, we write z ∼ N(0, 1).
   
• In general, x ∼ N(μ, σ²) means that x has a normal density with mean = μ and variance = σ².
   
• An inflection point are the points x on a curve f(x) where the second derivative equals zero: f"(x) = 0.
   
  
   
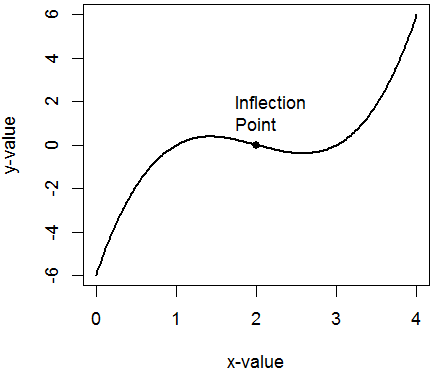
  Inflection points are where the concavity of the curve changes from concave up to concave down, or vice versa.
   
• On the standard normal curve, the inflection points are located one standard deviation away from the mean at x = ±1:
   
  
   
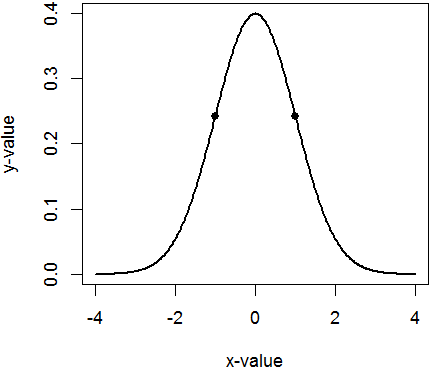
  For an arbitrary normal density, the inflection points are located at x = μ ± σ.

Introduction to SAS and R

• SAS has good built in capability for presenting the results of statistical analyses.
   
• R is a good programming language for customizing statistical calculations and for performing interactive calculations.
   
• Introduction to SAS
   
• Introduction to R
   
• ExamSco Example

The NIST Example

• NIST Example (National Institute of Standards and Technology).
   
• The job of the NIST to weigh the country's prototype weights to insure that the scales to measure these weights, the storage conditions, and the weighing procedures are all working properly.
   
• In spite of extreme care, sometimes a prototype weight will gain or lose weight unexpectedly, as this article discusses:
   
  
  Official Kilogram Prototype Mysteriously Losing Weight

Normal Plots

• We will discuss normal plots next time on Wednesday, July 19.
   
• We know that a normal distribution has an approximately bell-shaped histogram.
   
• in practice, it is often difficult to look at a histogram and determine how close its distribution is to normal, especially if the sample size n is small.
   
• An easier way to tell if a dataset is normally distributed is to look at the normal plot. If the normal plot is close to a straight line, the distribution of the dataset is close to normal.
   
• A normal plot is a scatterplot of the sorted actual data values (y-axis) vs. the expected normal scores (x-values).
   
• The NIST Example shows examples of normal plots in SAS and R.
   
• Here are sketches of five normal plots and their interpretations.
   
• If n is the number of observations, to compute the normal scores using Van der Waerden's method, find the z-scores that divide the standard normal curve into n + 1 equal areas.
   
• Practice Problem: Compute the normal scores of a dataset with 9 observations.
   
  Ans: The normal scores when n = 9 divide the standard normal curve into n + 1 = 10 equal areas like this:
   
  
   
  Look in the body of the normal table for these cumulative probabilities: 0.1000, 0.2000, 0.3000, 0.4000, 0.5000, 0.6000, 0.7000, 0.8000, and 0.9000. The closest matches are 0.5000, 0.5987, 0.6985, 0.7995, 0.8997. They have corresponding z-scores -1.28, -0.84, -0.52, -0.25, 0.00, 0.25, 0.52, 0.84, and 1.28.  Here are three SAS and R scripts to find normal scores.  They both find the normal scores -1.2815516, -0.8416212, -0.5244005, -0.2533471, 0.0000000, 0.2533471, 0.5244005, 0.8416212, 1.2815516.
   
• Use the R function qqnorm to create a normal plot:
  

  > x = rnorm(200)
  > qqnorm(x)
  

• There exist formal tests of hypothesis to check if a given sample comes from a normal distribution. Sas provides the results of these tests with proc univariate.
   
• The NIST Example shows the SAS output of the Kolmogorov-Smirnov, Cramer-von Mises, and Anderson-Darling tests for normality.
   
• To interpret these tests at the 0.05 level of significance. If p < 0.05, reject the null hypothesis that the sample comes from a normal distribution; if p > 0.05, accept it.
   
• The problem with tests of normality in general is that it is difficult to find a test statistic that distinguishes normal from non-normal distributions in all cases, especially for small samples.
   
• Most statisticians find the normal plot to be more useful than tests of normality for checking whether a sample has an approximately normal distribution.

The Boxplot

• We did not discuss this section on class. Read it if you need a review on the details of boxplots.
   
• The boxplot was invented in 1969 by the Princeton statistician John W. Tukey (1915 - 2000).
   
• The boxplot shows this information for a dataset: the first quartile Q1, the second quartile Q2, and the third quartile Q3, extreme outliers marked by *, and mild outliers marked by O.  Here is an example boxplot for the hypothetical exam scores
   
  
  5  39  75  79  85  90  91  93  93  98
  
  
• Let n be the number of observations, and let x_(i) be the ith observation of the sorted dataset. Then Q1, Q2, and Q3 can be defined by the Tukey's Hinges method like this:
   
  
  Q2 is the 2nd quartile = 50th percentile = the median. It is the middle observation x_(n+1)/2 of the sorted dataset when n is odd. It is the average of the two middle observations (x_n/2 + x_n/2+1) / 2 when n is even.
   
  Q1 is the 1st quartile = 25th percentile. The Tukey's Hinges method defines Q1 as the median of the bottom half of the data, where the bottom half of the data is defined by x₍₁₎, ... , x_(n/2) when n is even. The bottom half of the data is defined by x₍₁₎, ... , x_((n+1)/2) when n is odd. Note that when n is odd, the middle observation of the dataset is included in both the bottom half and the top half of the data.
   
  Q3 is the 3rd quartile = 75th percentile. The Tukey's Hinges method defines Q3 as the median of the bottom half of the data, where the bottom half of the data is defined by x_(n/2+1), ... , x_(n) when n is even. The bottom half of the data is defined by x_((n+1)/2), ... , x_(n) when n is odd. Note that when n is odd, the middle observation of the dataset is included in both the bottom half and the top half of the data.
  
  
• There are several other methods for computing percentiles of datasets. R provides nine different methods for computing percentiles; SAS provides five different methods of computing percentiles. Here is a link to the help page of the R quantile function.

Projects

• Project 1
   
• Final Project

Tests of Hypothesis

These last three sections on hypothesis tests will be discussed next time on Wednesday, July 19.

• Some sample research questions:
   
  
  1. Do vaccines for children cause autism?
      
  2. Do the electric and magnetic fields in high voltage electric power lines cause health risks for those living nearby?
      
  3. Is there a difference in network traffic speed between our existing router, and the new router that management is considering?
      
  4. Is the level of mercury intake for wading birds in the Florida Everglades declining? (Mendenhall and Sincich, p. 49)
      
  5. Does being on a low-fat diet cause people to lose more weight than those on a regular diet? (Mendenhall and Sincich, p. 53)
      
  6. Do red light cameras installed in a traffic intersection affect the number of vehicle collisions in that intersection? (Mendenhall and Sincich, p. 53)
  
  
• These research questions phrased as null hypotheses:
   
  
  1. There is no significant difference between the rate of autism for vaccinated children vs. the rate of autism for non-vaccinated children?
      
  2. There is no significant difference between the incidence of cancer higher for persons living close to electric power lines vs. the rate of cancer for persons that to not live close to electric power lines?
      
  3. There is no significant difference in network traffic speed between our existing router and the proposed new router?
      
  4. There is no significant difference of mercury intake for wading birds in the Florida Everglades between last year and this year?
      
  5. There is no significance of difference in weight loss between people on a low-fat diet vs. those on a regular diet?
      
  6. There is no significant difference in the occurrence of vehicle crashes between those intersections that have red light cameras installed vs. those that do not.
  
  
• Usually the researcher wants to reject the null hypothesis to show that the effect being investigated causes a real difference, and is not just chance variation.

Some Terminology

• A simple random sample consists of randomly selected subjects from a population where every subject is equally likely to be selected.
   
• A treatment group is a group of subjects that are manipulated using a medicine, chemical, or other process being investigated.
   
• A control group is a special type of treatment group. It receives no special medicine, chemical, or process, but leaves the random sample as is.
   
• To prevent a patient from knowing whether he or she is in the treatment or control group, patients in clinical trials are usually given a placebo.
   
• A statistical experiment with two treatment groups can have a treatment group and a control group or two different treatment groups.
   
• The response variable is the outcome or measurement obtained from a statistical experiment.
   
• A one-sample test of hypothesis tests whether there is a significant difference between the responses of the treatment group and the responses of the general population.  The response of the population value is obtained from a previous studies, expert knowledge, or theoretical calculations.
   
• For a one-sample z- or t-test, the null hypothesis (H₀) states that the variation in the test statistic is just chance variation.
   
• For a one-sample z- or t-test, the alternative hypothesis (H₁) states that the the difference between the test statistic and zero is too large to plausibly be chance variation (the difference is significant).
   
• A two-sample test of hypothesis tests whether there is a significance between the responses of the two treatment groups.
   
  
  A paired two-sample test has a natural pairing between the subjects in the two treatment groups. Necessarily, in this case, the two groups must be the same size.
   
  An independent two sample test  has no natural pairing between the subjects. The two treatmant groups need not be the same size.
  
  
• For a two-sample test, the null hypothesis (H₀) states that the difference between the treatment groups is due to chance variation; there is no significant difference between the groups.
   
• For a two-sample test, the alternative hypothesis (H₁) states that difference between the treatment groups is too large to plausibly be chance variation (the difference is significant).
   
• A test statistic T is a value computed from the data and the null hypothesis. For a one-sample z-test, the test statistic is
   
  
  z = (x - μ) / SE_mean
  
  
• The level α of a test of hypothesis is the probability of rejecting H₀ if, in fact, H₀ is true. Traditionally, the level of a statistical test is taken to be 0.05 or 0.01.
   
• A 100(1-α)% confidence interval I is an interval such that T ∈ I 100(1-α)% of the time if H₀ is true.
   
• The p-value of a statistical test is the probability of obtaining a test statistic value as extreme or more extreme than the value actually obtained, given that H₀ is true.
   
• The rejection region for a statistical test is the set of values of the test statistic T that lead the researcher to reject the null hypothesis H₀ and accept the alternative hypothesis H₁. For any value of T in the rejection region, p < α, where p is the p-value and α is the level of the test.
   
• The acceptance region for a statistical test is the set of values of the test statistic T that lead the researcher to accept the null hypothesis H₀ and reject the alternative hypothesis H₁. For any value of T in the rejection region, p ≥ α, where p is the p-value and α is the level of the test. If H₀ is accepted, it does not necessarily mean that the researcher believes it is true, it may only mean that there is not enough evidence to reject H₀.
   
• The power of a statistical test is the probability of rejecting H₀ (whether is it is true or false). Increasing the sample size always increases the power of the standard statistical tests.

The Five Steps of a Hypothesis Test

1. State the null hypotheses H₀ and the alternative hypothesis H₁.
    
2. Compute the test statistic T.
    
3. Compute a (1-α)100% confidence interval I for the test statistic T, where α is the level of the hypothesis test.
    
4. If T ∈ I, accept H₀ (and reject H₁); if T ∉ I, reject H₁ (and accept H₀).
    
5. Compute the p-value for T. In most cases p must be computed using statistical software.

T-tests of Hypothesis for One or Two Groups

• Descriptions of some tests of hypothesis for experimental designs that have one or two groups.
   
• Descriptions of tests with examples:
   
  
  1. One-sample z-test
      
  2. One-sample t-test
      
  3. Paired-sample z-test
      
  4. Paired-sample t-test   (Will be discussed on Monday, 6/27.)
      
  5. Independent Two-sample z-test
      
  6. Independent Two-sample t-test   (Will be discussed on Monday, 6/27.)
  
  
• There are two approaches to the independent two-sample t-test:
   
  
  1. Assume the variances of the two groups are equal, as described by the documents in the preceding link.
      
  2. Assume the variances can be different. This is called the Behrens-Fisher Problem, which we do not discuss in detail. Both SAS and R handle also handle the case of unequal variances. Both use Satterthwaite-Welch approximation, which can result in fractional degrees of freedom.