Suppose that the two groups are labeled A and B:
- Write down the null and alternative hypothesis:
H0: μA = μB - Compute the test statistic:
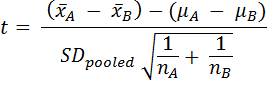
where

- Find a 100(1 - α)% confidence interval I for t. Use nA + nB - 2 degrees of freedom.
- If t ∈ I, accept the null hypothesis H0; if t ∉ I, reject the null hypothesis and accept the alternative hypothesis H1.
- Use SPSS to obtain the p-value.
To perform the independent two-sample t-test with SPSS, do the following:
Import the CalciumBloodPressure dataset into SPSS.
Set the Value Label to Calcium for Group 0 and to Placebo for Group 1.
Select Analyze >> Compare Means >> Independent Samples T-Test
In the Independent Samples T-Test Dialog, drag Decrease into the Test Variables box. Also, drag Group into the Grouping Variables box.
Click the Define Groups box. Enter 0 for Group 1; enter 1 for Group 2. Click Continue.
Click OK.
Here are the results. Look in the Independent Samples T-Test results in the first row: equal variances assumed:
t = 1.634 df = 21 Sig. (2-tailed) = 0.096.
This means that the p-value is 0.096: we reject the null hypothesis if we are testing at the 5%-level.
- H0: μ0 = μ1
H1: μ0 ≠ μ1 - n0 = 10 x0 = 5.00 SD0+ = 8.743
n1 = 11 x1 = -0.273 SD1+ = 5.901
SDpooled2 = [(n0 - 1)s02 + (n1 - 1)s12] / (n0 + n1 - 2)
= [(10 - 1)8.743 + (11 - 1)5.901] / (10 + 11 - 2) = 54.536
SDpooled = √54.536 = 7.385
t = (x1 - x0) / [SEpooled sqrt(1 / n0 + 1 / n1)]
= [5.000 - (-0.273)] / [7.285 sqrt(1/10 + 1/11)]
= 5.273 / (7.385 · 0.437) = 1.634 - The degrees of freedom are df = n0 + n1 - 2 = 10 + 11 - 2 = 19. Find a 95% confidence interval (0.025 upper tail area) from the t-table: I = [-1.729, 1.729].
- t = 1.634 ∉ [0, 1.729], so we accept H0: we do not have enough evidence to reject the null hypothesis.