To Documents
Final Exam Practice Problems 1
Multiple Choice Questions
For each question, show your work or give a reason explaining your answer.
4 points for the reason, 1 point for the correct answer.
- Roger Cotes was the first to publish a study on
- how well IQ scores fit the normal distribution.
- the applications of probability to economics.
- the theory of errors in astronomy.
- the uses of statistics in genetics.
Ans: b.
- Which of these is another name for categorical variables?
a. Continuous
b. Nominal
c. Ordinal
d. Scale
Ans: b. Nominal means that the data is not numbers. This is the
term used in SPSS.
- If Q1 = 1,230 and Q3 = 5,238, using the boxplot, the observation at
11,389 is
a. a mild outlier
b. an extreme outlier
c. below the 75th percentile
d. the median
Ans: a. IQR = 4,098. The inner fence to the right is at
Q3 + 1.5 * IQR = 11,385. The inner fence to the right is at
Q3 + 3.0 * IQR = 17,532. 11,389 is between the inner and outer fences,
so it is a mild outlier.
- What percentage of IQ scores are over 160,
assuming that IQ scores are normally distributed?
a. 0.32%
b. 0.032%
c. 0.0032%
d. 0.00032%
Ans: c: 0.0032%.
- For the curve shown below, the points shown in red are
a. asymptotes
b. critical points
c. inflection points
d. outliers
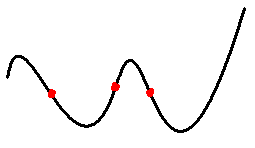
Ans: c: inflection points.
- The residual plot that we use in it223 consists of
- residuals plotted vs. normal scores
- residuals plotted vs. observation number
- residuals plotted vs. predicted values
- y-values plotted vs. x-values
Ans: c. Definition of residual plot.
Short Essay Questions
For full credit, use complete sentences and paragraphs. Your
explanation should make sense to someone that does not understand
statistics, like your mother.
- What is a histogram and in which situations is it useful?
What are the tradeoffs of using a histogram with many bins vs. a histogram with few bins?
- What is the difference between the mean and the median?
In which situations should each be used?
Problems
Show all of your work. You may use a calculator.
- Given the following data, draw the box plot.
Q0 = 0.001
Q1 = 0.035
Q2 = 0.057
Q3 = 0.089
Q4 = 0.311
Additional outliers are at 0.141, 0.189, 0.217, 0.240. You decide whether they
are mild or extreme.
Ans: See Review Problem 9 of the 7/22 notes.
- Given this table of grouped data, do the following:
| Bin | Percentage of Observations |
| [1,3] | 30% |
| (3,4] | 40% |
| (4,5] | 20% |
| (5,6] | 0% |
| (6,10] | 10% |
- Draw the histogram.
- Compute Q1, Q2, Q3 and IQR.
Ans: Q1 = 1.167, Q2 = 2.00, Q3 = 4.00, IQR = Q3 - Q1 = 4 - 1.167 = 2.833
- Compute the mean using a weighted average.
Ans: 2.7
- What percentage of the observations are greater than 2.5?
Ans: 77.5%.
- Compute the correlation of this dataset:
x: 1 2 3 4 5
y: 2 4 7 3 4
Here are the z-scores:
zx:
-1.414 -0.707 0.000 0.707 1.414
zy:
-1.195 0.000 0.000 -0.423 0.000
Ans: r = 0.2536
SPSS Analysis
Perform the following analyses with SPSS. Save your output file
as a Word .doc file. Type any interpretation of the output into the
output file itself.
- Input the Excel file
tv-gpa.xlsx into SPSS.
- Supply labels to the variables as follows:
| Variable Name | Label |
| Hours | Hours spent watching TV per week |
| HS_GPA | High School GPA |
- Determine the following for Hours and HS_GPA:
Q0
Q1
Q2
Q3
Q4
mean
SD+
Ans:
Using Tukey's Hinges for Percentiles
Hours: Q0=1.9
Q1=2.5
Q2=2.9 Q3=3.3
Q4=3.7
mean=2.871
SD+=0.5130
HS_GPA:
Q0=2
Q1=5
Q2=9
Q3=14
Q4=14
mean=9.71
SD+=5.425
- Create the boxplot for Hours and HS_GPA. Ans: Use SPSS.
- Determine the correlation between Hours and HS_GPA. Ans: -0.626
- Which is the independent variable? which is the dependent variable? Ans:
Hours, HS_GPA
- Compute and interpret the r-squared value. Ans: 0.00392.
R2 is the
proportion of variation in the dependent variable that can be attributed to the
independent variable.
- Find the regression equation for predicting the dependent
variable from the independent variable.
Ans: HS_GPA = -0.006 · Hours + 2.931
- What is the predicted highschool GPA for someone that watches
TV 40 hours per week. Why is this prediction not likely to be very
accurate?
Ans: 2.691. Because R2 is large.
- Create and interpret the residual plot. Use SPSS
- Create and interpret the normal plot of the residuals. Use SPSS
