To Notes

IT 223 -- May 22, 2024

Review Exercises

  1. List the formulas that we have discussed related to random variables and probability. Answer:
    1. -- If events A and B are independent, P(A and B) = P(A) * P(B)
    2. -- If events A and B are mutually exclusive, P(A or B) = P(A) + P(B)
    3. -- If A1, A2... , An are independent events with P(A1) + P(A2) + ... + P(An) = p,
      the probability that at least one of these events occurs is 1 - (1 - p)n.
    4. -- For a Bernoulli random variable X, E(X) = p, Var(X) = p(1 - p).
    5. -- For a Binomial random variable X, E(X) = np, Var(X) = np(1 - p).
    6. -- If X1, ... , Xn are random variables and S = X1 + ... + Xn with the same distribution, E(S) = n * E(X1).
    7. -- If X1, ... , Xn are independent random variables and S = X1 + ... + Xn with the same distribution, Var(S) = n * E(X1).
    8. -- The standard deviation σX of a random variable is √Var(X)
  2. What do these R functions do?
          rbinom  dbinom  pbinom    . Answer:

    rbinom(reps, n , p) generates simulated random outcomes from a binomial random variable with n trials and probability of success p. The argument reps determines the number out binomial outcomes, which is the number of times that the experiment is repeated.

    dbinom(k, n, p) is the height of the binomial density (probability) for k successes where n is the number of trials and p is the probability of success.

    pbinom is the area under the normal density, in other words, the probability for 0, 1, ... , k successes where n is the number of trials and p is the probability of success.
  3. If the probability of getting a cold in a given week is 3%, what is the probability of getting at least one cold in a year (52 weeks)?
    Ans: 1 - (1 - p)n = 1 - (1 - 0.03)52 = 0.7948 = 79.5%.
  4. Two 17th century dice games. Chevalier de Méré was a French nobleman that liked to bet on dice games. In particular, he bet on these two events: (a) in 4 rolls of a die, at least one ace (one) occurs, (b) in 24 rolls of a pair of dice, snakeeyes (double ones) occur at least once. Chevalier reasoned that since rolling an ace with one dice roll was 1/6, rolling at least one ace in four rolls of a die is 1/6 + 1/6 + 1/6 + 1/6 = 4/6 = 2/3 = 66.7%. He also reasoned that rolling snakeeyes in one roll of a pair of dice is 1/36, so the probability of rolling at least one snakeeyes in 24 rolls is 24 * 1/36 = 24/36 = 2/3. However, he knew from playing these games that Event (a) was more likely than event (b). Blaise Pascal used probabilty theory to calculate the true probabilies of events (a) and (b). Calculate these probabilities.
    Answer for Game (a): 1 - (1 - 1/6)4 = 0.5177 = 51.8%
    Answer for Game (b): 1 - (1 - 1 / 36)24 = 0.4914 = 49.1%
  5. Simulate these two dice games using R. Answer:
    > rbinom(4, 1, 1/6)
[1] 0 0 1 0
> rbinom(24, 1, 1/36)
[1] 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
  6. Is it possible for two events to be both independent and mutually exclusive at the same time?
    Ans: If A and B are independent, P(A and B) = P(A) P(B). But if A and B are mutually exclusive, P(A and B) = 0. Thus P(A) P(B) = 0 and either P(A) = 0 or P(B) = 0.
  7. Estimate the probability that an amateur golfer that plays once a week makes at least one hole in one on the fly on a certain par 3 hole in 50 years. The golfer hits the green 10% on that hole of the time, which has an area of about 4,000 square feet. The hole on a golf green has a radius of 4.25 inches.
    Ans: First estimate the probability of a hole in one in a single try. The area of the hole in square feet pi*(r / 12)2 = pi * (4.25 / 12)2 = 0.3941 ft2. If the area of the green is 4000 ft2, the probability of a hole in one in one shot is the area of the hole divided by the area of the green: 0.3941 / 4000 = 9.8525 * 10-5.
    The probability of getting at least one hole in one in 50 years is
          1 - (1 - 9.8525 × 10-5)(50 * 52) = 0.2259955 = 23%.
  8. The expected value of a random variable X is 15. What is the expected sum of 100 outcomes of X?
    Answer: E(S) = n * E(X) = 100 * 15.
  9. The theoretical SD of a random variable is 3. What is the theoretical standard error of the sum of 100 independent outcomes of X?
    Ans: σS = √n σx = √100 * 3 = 30.
  10. An American roulette wheel contains 38 pockets: 18 red pockets, 18 black pockets, and two green pockets labeled 0 and 00. European roulette wheels have only one green pocket labeled 0.
    If you bet on red or black, here are the payoff tables for an American roulette wheel, for a bet of $100:
    Bet on Red
    Outcome Payoff Probability
    Red +100 18/38 = 0.474
    Black -100 18/38 = 0.474
    Green -100 2/38 = 0.052

    Bet on Black
    Outcome Payoff Probability
    Red -100 18/38 = 0.474
    Black +100 18/38 = 0.474
    Green -100 2/38 = 0.052

    What is the expected payoff of playing on red? playing on black?
    Ans: Playing on red is E(x) = 100(0.474) + (-100)(0.474) + (-100)(0.052) = -5.20. You expect to lose about $5.20 each time you play on red with a $100 bet; same for black.
  11. The following boxes contain 6 tickets each. In which urns are letter independent from color. In other words, in which urns are the probabilities of the letters the same whether or not you know the color.

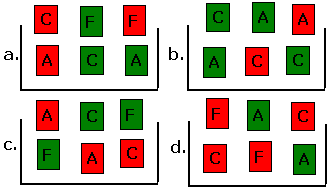
    Independence of color and letter
    Answer: In a and b, letter is independent of number. To show that letter and number are independent, you need to show that for each letter value L P(L) if you don't know the color = P(L) for a given color. For example, in Problem 8a, if you don't know the color, P(A) = P(B) = P(C) = 2/6 = 1/3. If you know the color is red, P(A) = P(B) = P(C) = 1/3. If you know the color is green, the probabilities are also 1/3.
    In Problem 8c, if you don't know the color, P(F) = 2/6 = 1/3. If you know that the color is green, P(F) = 2/3 = 2/3, so color and letter are not independent.
    To show that two events are not independent, it is enough to find one case where the probabilities are different; to show that two events are independent, you must show that the probabilities are the same for all choices of color and letter.
  12. Are these events independent?
    Person A lives at least 20 more years after June 1, 2024.
    Person B lives at least 20 more years after June 1, 2024.
    Ans: It is hard to know. If the people know each other, their lives and life choices can affect each other so A and B are probably not independent. If the people do not know each other, A and B may be independent, but they may also be related in unexpected ways.
  13. The probability that the Cubs can beat Team A in a single game is 60%. What is the probability that they win 7 or more games in a 10 game series with Team A?
    Answer: dbinom(k, n, p) = nCk pk (1 - p)n-k = 10C7 0.67 (1 - 0.6)10-7 = 120 * 0.0279936 * 0.064 = 0.2149908 = 21%
  14. Candidates A and B are running for mayor in a large city. A random sample of 400 persons are interviewed. 227 of them say they will vote for Candidate A. Find a 95% confidence interval for the true probability that a voter will vote for Candidate A. Also find a 99% confidence interval for this probability.
    Answer: n = 400, S = 227, E(S) = nE(X) = 400p,  p^ = 227/400 = 0.5675,
          σ^S = √(n * p^ * (1 - p^) = √(400 * 0.5675 * (1 - 0.5675) = 9.908456.
          zS = (S - E(s)) / σ^S = (227 - 400 * p) / 9.908456
    Now, by the central limit theorem, zS is normally distributed, so -2 ≤ zS ≤ 2  95% of the time. Solve for p:
    -2 ≤ zS ≤ 2
    -2 ≤ (S - E(s)) / σ^S ≤ 2
    -2 ≤ (227 - 400 * p) / 9.908456 ≤ 2
    -2 * 9.908456 ≤ (227 - 400 * p) ≤ 2 * 9.908456
    -2 * 9.908456 - 227 ≤ -400 * p ≤ 2 * 9.908456 - 227
    -246.8169 ≤ -400 * p ≤ -207.1831
    0.6170423 ≥ p ≥ 0.5179577
    This means that the 95% interval is [0.5179577, 0.6170423] or [52%, 62%]