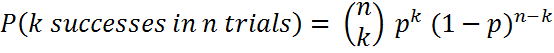To Notes

IT 223 -- May 20, 2024

Review Exercises

1. If A and B are two events, what must be true for
         P(A and B) = P(A) * P(B)
   to be true?
   Answer: A and B must be independent.
2. If A and B are two events, what must be true for
         P(A or B) = P(A) + P(B) to be true?
   Answer: A and B must be mutually exclusive.
3. How is the variance related to the standard deviation of a dataset or of a random variable?
   Answer: The variance is the square of the standard deviation.
4. What is the variance of a discrete random variable?
   Answer: if P(X=x_i) = p_i for each i,
   Var(X) = (x_i - E(X))² * p₁ + ... + (x_n - E(X))² * p_n
5. What is the expected value of a Bernoulli random variable?
   Answer: for a Bernoulli random variable, P(X = 0) = 1 - p and P(X = 1) = p. Then
   E(X) = x₁ P(x₁) + ... + E(X) = x_n P(x_n) = 0 * (1 - p) + 1 * p = p,
   so that E(X) = p.
6. What is the variance of a Bernoulli random variable?
   Answer: Var(X) = (x₁ - E(X))² * p₁ + ... + (x_n - E(X))² * p_n =
         (0 - p)² * (1 - p) + (1 - p)² * p = p * (1 - p) * (1 - p + p) = p * (1 - p), so
         Var(X) = p * (1 - p)
7. If S is the sum of n independent outcomes x₁, ... , x_n from a random variable X, what are E(S) and Var(S) in terms of E(X) and Var(X)?
   Answer: E(S) = E(X₁ + ... + X₁) = E(X₁) + ... + E(X_n) = nE(X), so E(S) = nE(X)

Using R to Simulate Bernoulli Outcomes

1. Use R to simulate the random outcomes from flipping a fair coin 10 times. Answer: the probability experiment is flipping a coin once; this experiment is repeated 10 times. A binomial random variable is specified number of independent outcomes from a Bernoulli random variable.

   // Here are the meanings of the R arguments:
   // n = number of times the experiment is repeated
   // size = number of Bernoulli outcomes in one experiment
   // prob = the probability of success for Bernoulli rv.
   rbinom(n=10, size=1, prob=0.5)
    [1] 1 0 0 1 1 1 1 0 0 1
   

2. Use R to simulate 20 repetitions of flipping a coin 2 times.
   Answer: in this case, n = 20, size = 2, and prob = 0.5.
   

   > rbinom(n=20, size=2, prob=0.5)
   # or
   > rbinom(20, 2, 0.5)
    [1] 1 2 1 2 0 1 1 1 0 2 0 2 2 2 0 1 1 1 1 1
   

3. Use R to simulate flipping a fair coin one million times. Repeat the experiment twice. Answer:
   

   > > rbinom(2, 1000000, 0.5) 
   [1] 500664 499815
   

4. Elena Delle Donne is the best free throw shooter in WNBA history with a career average of 93.4%. Simulate 10 seasons of shooting 90 free throws per season with a success rate of 93.4%. Answer:
   

   > rbinom(10, 90, 0.934)
   [1] 79 82 84 87 86 81 85 86 82 87
   

The Law of Averages

• The official name of the Law of Averages is the Law of Large Numbers (LLN). It was first proved by Jakob Bernoulli from Basil, Switzerland in 1713.
• LLN states that if x₁, ... , x_n are independent outcomes of the same random variable x and n is large enough, then the average x is close to the expected value E(x) = E(x) with high probability.
• LLN works by swamping, not by compensation. What does this mean?
  Ans: It means that if the average of outcomes of a random variable is larger than the expected value of the average, there is no reason to expect that if you continue to collect outcomes from the random variable that those new outcomes will be smaller than the expected value of the average to compensate.  Instead it means that by swamping the average with many more outcomes, the new outcomes will be close to the average with high probability, so the overall average will also tend to be closer to the expected value. Note that this is true with high probability; there will always be a small probability that the overall average is not close to the expected value of the average.
• Experiment: Use R to simulate 100, 1000, and 10,000 tosses of a fair coin. Are the averages obtained consistant with LLN?
  Ans: Here are the results:
  
  

  n	S	x
  1,000	469	0.4690
  10,000	4,925	0.4925
  100,000	49,781	0.4978
  1,000,000	500,107	0.5001

The Central Limit Theorem

• Even if a random variable x is not normally distributed, both the sum S and average x of n independent outcomes of a random variable are approximately normally distributed if n is large. Usually we say that n is large if n > 30.
• Example 24:   Flip a coin 1,000 times and obtain 514 heads. Find a 95% confidence interval for the true value p of obtaining a head. This will give us an idea if the coin is fair.
  Ans: Flipping a coin once is a Bernoulli random variable with P(X = 1) = p, so E(x) = p and σ_x = √p(1 - p). The sum of n independent Bernoulli random variables S is the number of heads; E(S) = np and σ_S = √np(1 - p). For computing σ_S, we don't know the value of p, so we estimate it with p^{^} = S / n = 514/1000 = 0.514. Therefore the estimated standard deviation is
  σ^{^}_S = √1000 * 0.514 * (1 - 0.514) = √249.804 = 15.81.
  Now a 95% confidence interval for z is -2 ≤ z ≤ 2. (More precisely, -1.96 ≤ z ≤ 1.96). We can solve for p:
       -2 ≤ z ≤ 2
       -2 ≤ (S - np) / σ^{^}_S ≤ 2
       -2 ≤ (514 - 1,000p) / 22.36 ≤ 2
       -44.72 ≤ 514 - 1,000p ≤ 44.72
       -44.72 - 514 ≤ - 1,000p ≤ 44.72 - 514
       -558.72 ≤ - 1,000p ≤ -469.28
  0.55872 ≥ p ≥ 0.46928
  This means that the 95% confidence interval is [0.46928, 0.55872] or [47%, 56%].

Factorials and Counting Combinations

• Recall that n! (read n factorial) is defined as
       n! = n × (n-1) × (n-2) × ... × 3 × 2 × 1
• n! is the number of ways of arranging n distict objects.
• 3! = 6. For example, the number of ways of arranging A, B, and C is
       (ABC)   (ACB)   (BAC)   (BCA)   (CAB)   (CBA)
• 2! = 2. The number of ways of arranging A and B is
       (AB)   (BA)
• 1! = 1. The number of ways of arranging the single object A is
       (A)
• What is 0!?

  Ans: There is exactly one way of arranging zero objects: ( ). Thus 0! = 1.

• The number of ways of drawing k objects from an urn that contains n distinct objects is
  
• The binomial coefficient defined in the previous bullet point is also written as nCk and read "n choose k."
• The binomial coefficients can also be obtained from Pascal's Triangle:
  

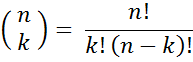
                      1
                   1     1
                1     2     1
              1    3     3     1
           1    4     6     4     1
        1     5    10    10    5     1
      1    6    15    20    15    6     1
    1   7    21    35    35    21    7     1
  1   8   28    56    70    56    28    8     1
  

• Each entry in Pascal's triangle can be obtained recursively by adding the two entries above it.
• nCk can be obtained from in Pascal's Triangle as entry k in row n.
• Practice Problems: How many ways are there of choosing
  
  1. 2 items from 3?
     Answer: 3C2 = 3! / 2!(3 - 2)! = 3*2*1 / ((2*1)1) = 3.
     The ways of choosing 2 items from 3 is (12), (13), (23): 3 ways.
     Using R:
     

     > choose(3, 2)
     [1] 3
     

  2. 3 items from 5?
     Answer: 5C3 = 5! / (3!(5 - 3)!) = (5*4*3*2*1) / ((3*2*1)(2*1) = 5*2 = 10.
     The ways of choosing 3 items from 5 is (123), (124), (125),(134),(135),(145),(234),(235),(245),(345):  10 ways.
     Using R:
     

     > choose(5, 3)
     [1] 10
     

  3. 5 items from 8?
     Answer: 8C5 = 8! / (5!(8 - 5)!) = (8*7*6*5*4*3*2*1) / ((5*4*3*2*1)(3*2*1)) = 8 * 7 = 56,
     Using R:
     

     > choose(8, 5)
     [1] 56
     

  4. 13 items from 20?
     Answer: 20C13 = 20! / (13!(20 - 13)!) = (20*19*18*17*16*15*14) / (7*6*5*4*3*2*1) = 19*17*16*15 = 77520,
     Using R:
     

     > choose(20, 13)
     [1] 77520
     

  Verify each of these values using the R choose function. Answer: see preceding problem.

Project 4

• Look at the Project 4 Description.
• Simulating repeated trials from a Bernoulli random variable using R:
       Method 1: Generate n values using rbinom(n, 1, p)
       Method 2: Generate one value using rbinom(1, n, p). The one value is the number of ones obtained, which is the sum of the outcomes.

The Binomial Theorem

• Suppose you have a Bernoulli distribution with p = probability of success. What is the probability of k successes out of n trials? Ans:
  
  
  
• This formula can also be written as
  P(successes in k trials) = nCk p^k (1 - p)^n-k
• Practice Problems:
  
  1. Flip 5 coins. What is the probability of obtaining exactly 3 heads?
     Answer: the probability is
     nCk p^k (1 - p)^n-k = 5C3 0.5⁵ (1 - 0.5)^{10 - 5} = 10! / (5!(10-5)!) * 0.125 * 0.25 = 0.3125.
     Using R:
     

      > dbinom(3, 5, 0.5)
     [1] 0.3125
     

  2. Roll a die 10 times. What is the probability of rolling exactly 5 ones?
     Answer: nCk p^k (1 - p)^n-k = 10C5 (1/6)⁵ (1 - 1/6)^10-5 =  
     10! / 5!(10-5)! *  0.0001286008 * 0.4018776 = (10*9*8*7*6)/(5*4*3*2*1) * 5.168178e-05 =
     (3*2*7*6) * 5.168178e-05 = 252 * 5.168178e-05 = 0.01302381.
     Using R:
     

     > dbinom(5, 10, 1/6)
     [1] 0.01302381
     

  3. Shoot 50 free throws, where the probability of success is 80%. What is the probability of hitting 45 or more free throws?
     Answer: perform the "hand" calculations with R:
     

     > choose(50, 45) * 0.7^45 * (1-0.7)^(50-45) +
     + choose(50, 46) * 0.7^46 * (1-0.7)^(50-46) +
     + choose(50, 47) * 0.7^47 * (1-0.7)^(50-47) +
     + choose(50, 48) * 0.7^48 * (1-0.7)^(50-48) +
     + choose(50, 49) * 0.7^49 * (1-0.7)^(50-49) +
     + choose(50, 50) * 0.7^50 * (1-0.7)^(50-50)
     [1] 0.0007228617
     > # Next compute these probabilities with dbinom:
     > dbinom(45, 50, 0.7) + dbinom(46, 50, 0.7) + dbinom(47, 50, 0.7) + 
     + dbinom(48, 50, 0.7) + dbinom(49, 50, 0.7) + dbinom(50, 50, 0.7)
     [1] 0.0007228617
     > # Finally pbinom(44, 50, 0.7) computes the probability of 
     > # making 44 or fewer free throws.  1 - pbinom(44, 50, 0.7) is
     > # the probability of making 45 or more free throws:
     > 1 - pbinom(44, 50, 0.7)
     [1] 0.0007228617