Part 1. Text Categorization

In this problem you will explore two approaches for automatic text categorization (a.k.a. document classification). You will first implement a basic multinomial Naïve Bayesian classifier. Then you will implement a simple document classifier based on the Rocchio method (adapted for classification). For both methods you will use this modified subset of BBC News stories to train and test your classifiers. The assignment dataset consists of an already processed set of 2225 documents from the BBC news website corresponding to stories in five topical areas from 2004-2005. Each document is represented as a feature vector over a set of 6167 features (after tokenization, stop word removal, stemming, and frequency filtering). Each document belongs to one of 5 classes (business, entertainment, politics, sport, tech). The data has already been split (80%, 20%) into training and test data both of which are provided in document x term matrix format containing a row for each document and a column for each feature in the vocabulary (note, however, that the first column of each row represents the documeet id in the original dataset, and this column should be removed to get the doc-term frequency matrices). The class labels for instances in the training and the test data are provided in separate files. Also, the set of features used in the data (representing the columns in the train and test matrices) is provided as a separate file. Please be sure to read the readme.txt file in the distribution for a more detailed description of the data.

1. [40 pts] Document Categorization Using Naïve Bayesian Classifier)
   
   Implement your own version of a Naïve Bayesian classifier. Your program should consist of two separate components: training and test. The training component, NB_Train(train_matrix, train_class_labels),  learns from the training data by computing the priors for each class and the conditional (posterior) class probabilities associated with different features (in this case terms in the vocabulary). The test component, NB_classify(posteriors, priors, test_instance),  uses the learned model (posterior and prior probabilities returned by the training function) to classify a test instance that was not used for training. Your program should work for any number of classes and not just for the number of classes in the provided data set.  Note: to avoid floating point underflow, you should use the sum of log probabilities when computing the class labels using Bayes's rule (for uniformity, please use natural log when computing the log probabilities).
   
   Your task is to train your classifier using the provided training data. Then you need to evaluate your classifier using the provided test data. For the latter task you should create an evaluation function to measure the accuracy of your trained classifier on the full test set. This function will apply your learned model returned from the training component to predict a class label for each of the test instances in the test data. Then for each test instance, it compares the actual test class label to the predicted class label. Your evaluation function should return the overall Classification Accuracy (ratio of correct predictions to the number of test instances in the full test set). It should also have the option to output the predicted class labels together with the sum of log probabilities for a portion of the test data (this is to illustrate that your classifier is working properly). Your program should also provide the capability to view the learned class probabilities for each class label and the posteriors for specified terms (again, this is to provide optional intermediate results demonstrating the proper functioning of your training function). In addition to your code, provide the following outputs as part of your submission (clearly identify which output corresponds to which part of the problem):
   
   
   1. After training your classifier, provide the prior probabilities associated with each class label.
      
      
   2. Based on your trained model, provide the posteriors (conditional class probabilities) for each of the following features:  "hollywood", "footbal", "comput", "labour". Note that this is Pr(feature | class) for each class. Here is an example output using the term "tax".
      
      
   3. Provide an output showing actual and predicted class labels for the first 20 document instances (instances 0-19) in the test data along with the log probability values for each test instance. For example, see this sample output for test instances 30-39.
      
      
   4. Using your evaluation function provide the overall classification accuracy across all test instances.
      
      

   ---

   
   
2. [20 pts] Document Categorization Using Rocchio Method
   
   Implement your own version of the Rocchio method for text classification discussed in class (See: Text Categorization - Part 1). This is a simple algorithm, but often produces good results in text classification tasks. You will train and test your implementation using the same BBC News dataset used in the previous problem. As before, you should separate the training function from the classification function. The training part for the classifier can be implemented as a function that takes as input the training data matrix and the training labels, returning the prototype vectors for each class. The classification part can be implemented as another function that would take as input the prototypes returned from the training function and the instance to be classified. This function should measure Cosine similarity of the test instance to each prototype vector. Your output should indicate the predicted class for the test instance and the similarity values of the instance to each of the category prototypes. Also, as in the previous problem, you should create an evaluation function that iterates over all test instances and report the overall classification accuracy. Your program should work for any number of classes and not just for the number of classes in the provided data set. Note: for this problem do not perform TFxIDF transformation of the data. You should use the original raw term counts in the provided training and test data sets. In addition to your code, provide the following outputs as part of your submission (clearly identify which output corresponds to which part of the problem):
    
   1. Provide an output showing actual and predicted class labels for the first 20 document instances (instances 0-19) in the test data along with the similarity of the test instance to the most similar class prototype. For example, see this sample output for test instances 30-39.
      
      
   2. Using your evaluation function provide the overall classification accuracy across all test instances.
      
      

Part 2. Hyperlink Analysis

In this part of the assignment you will explore well-known, simple, yet powerful hyperlink analysis methods. Specifically, you will implement your own versions of the HITS algorithm (Hubs and Authorities) and the PageRank algorithm. For this problem, you should not use external libraries that directly compute PageRank or hubs/authorities for a graph. For the purposes of this problem, you can represent a directed graph with an adjacency list (for each node p in the graph representing a Web page, the  adjacency  list for that node includes all the nodes to q to which p points i.e., there is a directed edge from p to q). For example, the simple directed graph, G, given below:

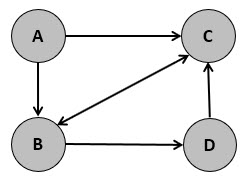
may be represented using the folllowing adjacency list:

G = {
    'A': ['B','C'],
    'B': ['C','D'],
    'C': ['B'],
    'D': ['C']
}

3. [20 pts] PageRank
   
   Implement the iterative version of PageRank algorithm given in lecture notes on Hyperlink Analysis (see slide 46). Your implementation should include a function  PageRank(G, alpha, num_iter) that takes the representation of any graph G, the PageRank damping factor, alpha, and maximum number of iterations, num_iter, and returns a vector R of PageRank values for each node in the graph (after the max number of iterations). Your function may optionally provide intermediate PageRank vectors at the end of each iteration (after the normalization step). For instance, using PageRank(G, 0.25, 5) with the above example graph may produce something similar to this sample output.
   
   To demonstrate your program, submit the output of your program on the following graph, G1, using alpha = 0.5 and number of iterations = 5.
   
                                                 
   
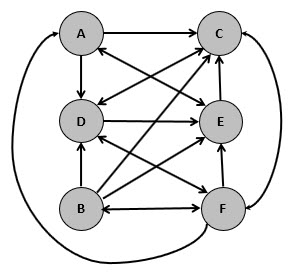
   The adjacency list for the graph is given below:
   

   G1 = {
       'A': ['C','D','E'],
       'B': ['C','D','E','F'],
       'C': ['D','F'],
       'D': ['C','E'],
       'E': ['A','C'],
       'F': ['A','B','C','D','E']
   }
   

   ---

   
   
4. [20 pts] HITS Algorithm (Hubs and Authorities)
   
   Implement the iterative version of HITS algorithm given in lecture notes on Hyperlink Analysis (see slide 27). The main component of your implementation should be a function, HITS(G, num_iter) which takes, as input, the representation of any graph G and the maximum number of iterations, num_iter, and returns two vectors: a vector A representing authority values for each node and a vector H representing the hub values for each node. These vectors represent the updated hub and authority values for the nodes in the graph after num_iter update cycles. Your function may optionally display intermediate hub and authority vectors at the end of each iteration (after the normalization step). You may find it helpful to have helper functions for updating the hub and the authority vectors during each iteration in the main function. As an example, using HITS(G, 5) with the aforementined example graph, G,  may produce something similar to this sample output.
   
   To demonstrate your program, submit the output of your program on the graph G1, from the previous problem, using num_iter = 5.