Notes on Logic Programming and Prolog
Bamshad Mobsher, DePaul
University
- The fundamental notion behind logic programming is to use
first-order logic as a programming language. First-order Predicate
logic is a formal language that allows for explicit representation
of information in the form of declarations (as predicates and
logical formulas). But, aside from its knowledge representation
capabilities, logic also has a procedural intepretation emanating
from it proof theory (i.e., application of rules of inference
to a set of formula to derive other formulas). Thus, the Power
of LP is in the synergism between logic (declarativeness) and
programming (procedurality):
- Kowalski's equation: Algorithm = Logic + Control
- Logic component: specification (What needs to be done)
- Control component: implementation (how it needs to be done)
- Example: Consider the algorithm for the factorial function
- Logic component (specification)
fact(n) = 1, if n = 0 fact(n) = n * fact(n-1), if n > 0
- Algorithm 1 (top-down):
input n; fact = 1; if n = 0 then return fact; fact = fact * n; n = n - 1; goto step 2;
- Algorithm 2 (bottom-up):
input n; fact = 1; n1 = 0; if n1 = n then return fact; n1 = n1 + 1; fact = fact * n1; goto step 2;
The two algorithms above specify two different "procedures" for the implementation of the factorial, but the logic component is always the same.
- Logic component (specification)
- In a Logic Programming System
- Logic provides a concise way to specify what the algorithm
should do. Programmer only specifies the logic component of the
algorithm:
fact(0, 1) /\
Forall x,n (n > 0 /\ fact(n-1, x) => fact(n, n * x)) - In Prolog-like notation, this is written as the two statements
(clauses):
fact(0, 1).
fact(n, y) :- fact(n-1, x), y = n * x
- Logic provides a concise way to specify what the algorithm
should do. Programmer only specifies the logic component of the
algorithm:
- Prolog Language Constructs
- Terms - constructed from constants, variables, function
symbols, e.g.,
tree(Left, Node, Right) mary, 1, "string", 3.14 successor(successor(1)) - Atoms (atomic formulas) - p(t1,t2,...,tn), where
p
is a predicate symbol and t1,...,tn are terms, e.g.,
valuable(gold) father(john, mary) sorted([3, 1, 2, 5], X)Atoms represent primitive declarations which evaluate to true or false. - Literals - atoms and their negation, e,g,
likes(tom, mary) ~isin(3, List) - Logical Connectives, Quantifiers, Formulas:
1st-order logic connectives:
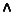 ,
, 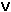 ,
, 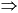 , ~,
, ~, 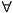 ,
, 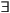 .
.
Formulas are made up from predicates and connectives:
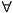 N ( natural(N) => natural(successor(N))
)
N ( natural(N) => natural(successor(N))
)
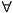 L1 ( list(L1) =>
L1 ( list(L1) => 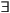 L2 (
sorted(L1, L2) ) )
L2 (
sorted(L1, L2) ) )
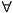 X,Y [
X,Y [ 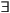 Z ( parent(X,Z) /\
parent(Z,Y) )
=> grandp(X,Y) ]
Z ( parent(X,Z) /\
parent(Z,Y) )
=> grandp(X,Y) ]
In logic programming, such formulas are often written in clausal form (backwards implication with implicit quantification):
natural(successor(X)) :- natural(X). grandp(X,Y) :- parent(X,Z), parent(Z,Y).In general, a clause is of the form:
A1,A2,...,Am :- B1,B2,...,Bmwhere
A1,...,A2(a disjuction of atoms) is called the head of a clause, andB1,...,Bm(a conjunction of literals) is called the body of the clause.Logic programming languages such as Prolog, use a special case form of clauses where the head of the clause is restricted to a single atom. Such clauses are called Horn clauses:
A :- B1,...,BmThe procedural interpretation of such a clause is: to solve a problem A, first solve B1, B2, ..., Bm. Comparison to procedural languages:
procedure A(...) call B1(...) call B2(...) ... call Bm(...) End;Clauses that have no body are called facts; other clauses are called rules. A logic program is simply a set of clauses.
- Terms - constructed from constants, variables, function
symbols, e.g.,
- Procedural Interpretation of Logic
This procedural interpretation came from the proof theory of first-order predicate calculus (applying rules of inference to axioms).
Example of inference rule (Modus Ponens):
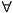 X ( human(X) => mortal(X) )
X ( human(X) => mortal(X) )
human(bob)
----------------------------------------
mortal(bob)Resolution (Robinson 1965) is the inference rule used in logic programming (suitable for derivation from clauses):
~P \/ Q P \/ R \ / \ / \ / Q \/ R (resolvant)To see how resolution is used in logic programming consider the following axioms:
mortal(X) :- human(X). human(bob).
To see if something is "mortal" (i.e., if
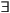 y [ mortal(y) ] is a logical consequence of
these axioms), assume the contrary (proof by contradiction):
y [ mortal(y) ] is a logical consequence of
these axioms), assume the contrary (proof by contradiction):
~ 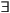 y [ mortal(y) ]
y [ mortal(y) ]or in clausal form (represented as a query):
?- mortal(Y).
and try to reach the empty clause (contradiction):
(goal) (program clause) ?- mortal(Y) mortal(X) :- human(X) | / {y=x} | / | / ?- human(X) human(bob) | / | / {x=bob} | / (empty clause)So, mortal(Y) is a logical consequence of this program with an answer substitution {y = bob}. This process of proof by contradiction is called the refutation procedure.Note that proofs are constructive: for factorial program, the query
?- factorial(4, X) will result in an answer {x = 24}. To sort a list with a program defining predicate sorted(X, Y) (i.e., y is the sorted version of x), the query
?- sorted([3,2,1], Z) will give:
{z = [1,2,3]}. The answer substitutions are the result of unification of terms during the deduction process. In the previous example, the second resolution step, attempts to unify the expression human(X) with the expression human(bob). This is accomplished by applying the answer substitution (X = bob} to the expression human(X).
- Substitution and Unification:
- Definition:
- A substitution is a finite set of equalities
{X1 = t1, X2 = t2, ..., Xn = tn} where each Xi is a variable and ti is a term, X1, ..., Xn are distinct variables, and Xi is distinct from ti. Each X i = ti is called a binding for Xi. Typically, we denote substitutions by the Greek letters
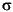 ,
, 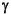 ,
, 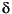 ,
, 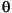 , etc.,
possibly subscripted.
, etc.,
possibly subscripted.
- Definition:
- Suppose
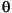 is a substitution and E is
an expression. Then
E
is a substitution and E is
an expression. Then
E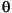 , the instance of E by
, the instance of E by
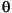 , is the expression obtained from E by
simultaneously replacing each occurrence of the variable
Xi in E by the term
ti, where Xi =
ti is a binding in the substitution
, is the expression obtained from E by
simultaneously replacing each occurrence of the variable
Xi in E by the term
ti, where Xi =
ti is a binding in the substitution 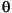 .
.
- Example:
- Suppose
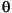 is the substitution {X = b, Y =
a},
is the substitution {X = b, Y =
a}, 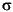 is the substitution {X = Y, Y = a},
and
is the substitution {X = Y, Y = a},
and 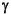 is the substitution {X = Y, Y = a, W =
b}.
Let E be the atom p(X,Y,Z). Then
is the substitution {X = Y, Y = a, W =
b}.
Let E be the atom p(X,Y,Z). Then
- E
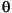 = p(b, a, Z).
= p(b, a, Z).
- E
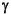 = p(Y, a, Z).
= p(Y, a, Z).
- E
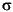 = p(Y, a, Z).
= p(Y, a, Z).
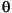 since
there is no binding of the form Z = t.
since
there is no binding of the form Z = t.
In the second case, it is important to observe that the replacement of variables by terms take place simultaneously. Thus the variable X in E is replaced by Y at the same time that Y is replaced by a. We do not further replace Y in the resulting expression by a to produce p(a,a,Z).
The last case illustrates that there may exist bindings in the substitution that do not have any effect on the expression. In this since E does not contain the variable W, the binding W = b in
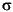 is superfluous.
is superfluous.
- E
- Definition:
- Suppose A and B are two expressions. A substitution
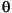 is called a unifier of A and
B if A
is called a unifier of A and
B if A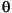 is syntactically identical to
B
is syntactically identical to
B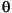 . We say A and B are
unifiable whenever a unifier of A and B exists.
. We say A and B are
unifiable whenever a unifier of A and B exists.
If, in addition,
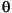 is the "smallest" possible
substitution which unifies two atoms, we say that
is the "smallest" possible
substitution which unifies two atoms, we say that 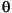 is
the most general unifier, usually written mgu. The word
"smallest" here means that for any other unifier
is
the most general unifier, usually written mgu. The word
"smallest" here means that for any other unifier 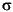 of
A and B, we can obtain A
of
A and B, we can obtain A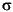 (or
equivalently B
(or
equivalently B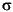 ) by further instantiating
A
) by further instantiating
A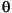 (or equivalently B
(or equivalently B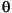 ).
).
Examples:
- The two expressions f(X,a) and f(a,b) unify with the
substitution {X = b}.
- The two expressions successor(successor(N)) and
successor(Y) unify with {Y = successor(N)}.
- The two expressions f(g(Y),X) and f(Z, h(b)) unify with
{Z=g(a), X=h(b), Y=a}. However, this is not the most general
unifier. The mgu in this case is: {Z=g(Y), X=h(b)}.
- The two expressions f(X,a) and f(b, g(Y)) are not
unifiable, since there is no substitution that can unify a (a
constant) and g(Y).
- The following two expressions are both structures representing binary
trees:
tree(tree(nil,2,nil),4,tree(tree(nil,5,nil),6,nil))
tree(tree(nil,X,nil),4,Right)They have the mgu: {X=2, Right=
tree(tree(nil,5,nil),6,nil)}.
- Resolution and Prolog's Computational
Model:
We can now describe a more general form of resolution which is used by Prolog in the computation process:
Given a query ?- Q1, Q2, ..., Qn, and a program clasue of the form:
A :- B1, B2, ..., Bm, such that A (the head of the clause) unifies with Q1 via the mgu
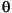 , then the resolvant:
, then the resolvant:
?- (B1, B2, ..., Bm, Q2, Q3, ..., Qn) 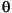
becomes the new subgoal in the next computation step.
Example: Consider the following Prolog program:
1. p(a, b). 2. p(a, c). 3. p(b, d). 4. p(c, e). 5. q(X, Y) :- p(X, Z), p(Z, Y).
In this program, the first four statements are facts (which are clauses without a body), and the last statement is a rule with two predicates on the right-ahnd-side. Now given the ground query
?- p(a b), it will immediately unify with the head of clause 1. In the Prolog interpreter, the effect would be as follows:?- p(a, b). yes
On the other hand a query
?- p(a, d)does not unify with the head of any clause:?- p(a, d). no
The non-ground query
?- p(a, X)unifies with the head of clauses (facts) 1 and 2. Prolog will first unify with clause 1 (resolvant will be the empty clause) using the substitution {X = b}. Prolog's search strategy allows for backtracking to the last subgoal satisfied. This happens automatically, if the current subgoal fails (there is no clause whose head unifies with the subgoal), or in case there is successful derivation of an answer, we can force Prolog to back t rack by using the ";" directive. In this example, ";" forces Prolog to backtrack to the original goal,?- p(a, X)and try to unify it with the head of another clause in the program. Here it will succeed with the substitution {X = c}:?- p(a, X). X = b; X = c; no
The query
?- q(a, W)will unify with the head of clause 5 via the mgu {W = Y, X = a}. So, the result of resolving?- q(a, W)andq(X, Y) :- p(X, Z), p(Z, Y)will be a new subgoal; the query?- p(a, Z), p(Z, W). This is a conjunctive query; Prolog will select the leftmost predicatep(a, Z)for the next resolution step. Now,p(a, Z)will first unify with the fact in clause 1 (p(a, b)) with the mgu {Z = b}.So, the result of resovling
?- p(a, Z), p(Z, W)andp(a, b)will be the new subgoal?- p(b, W). Finally, in the next resolution step,?- p(b, W)will unify with clause 3. (p(b, d)) with the substitution {W = d}, leaving the empty clause as the resolvant. The unifier {W = d} is returned as the answer to the original query?- q(a, W).If we now use ";" to force backtracking, Prolog will backtrack to the subgoal
?- p(a, Z), p(Z, W), which is the last subgoal that can be resolved with the head of a different clasue (this time clause 2:p(a, c)). The resolvant will be the new subgoal?- p(c, W), and in the next resolution step,?- p(c, W)will unify with clause 4. (p(c, e)) with the substitution {W = e}, leaving the empty clause as the resolvant. The unifier {W = c} is then returned as the second answer to the query?- q(a, W).You can verify that, in this case, further backtracking will not result in any new answers. We can depict this computation in the form of a full computation tree, as follows:
- Example: Consider the following
logic program
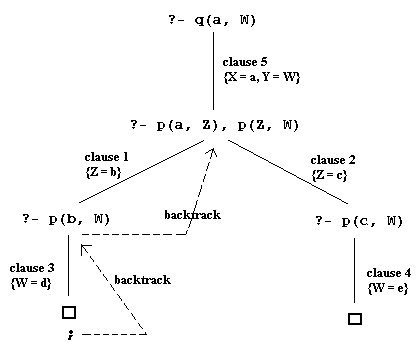
1. parent(a,b). 2. parent(b,c). 3. parent(c,e). 4. parent(a,d). 5. grand(U,V) :- parent(U,W), parent(W,V). 6. ancestor(X,Y) :- parent(X,Y). 7. ancestor(X,Y) :- parent(X,Z), ancestor(Z,Y).
Clauses 1-4 are facts and clauses 5-7 are rules. This program specifies the parent, grandparent and ancestor relationship. Note that the two clauses 6 and 7 together specify what it means for X to be an ancestor of Y. Clause 7 is an example of recursive rule
Now, if we give the system the query: ?- grand(X,Y), this can result in two possible answers. In Prolog interpreter, this will look like the following:
?- grand(X,Y). X = a Y = c; X = b Y = e; no. ?- ancestor(a, Y). Y = b; Y = d; Y = c; Y = e; no.
The (partial) computation tree for the above query is depicted below:
- Lists in Prolog:
Lists in Prolog are represented by square brackets. Prolog also allows for aggregate values of type lists. For example, when calling a predicate, we may pass a list containing elements a,b,c by typing
[a,b,c].
The empty list is represented by []. To define rules for manipulating lists, we need list constructors, as well as selectors for pulling apart lists. Prolog combines all of these operations into one, with the help of unification.Consider the following Prolog program for appending lists. It contains two rules.
append([],List,List). append([H|Tail],X,[H|NewTail]) :- append(Tail,X,NewTail).
A call to append requires three arguments. The natural way to view the intended use of the arguments is that the first two arguments represent the two lists that we want to append, and the third argument returns the result of the append. For example, if we pose the following query to append,?- append([a,b,c],[d,e],X).
we would get back the answer X = [a,b,c,d,e].The vertical bar symbol acts both as the constructor and selector for lists. When we write [X|Y], this represents a list whose head is X, and whose tail (i.e. the rest of the list) is Y. Based on this interpretation, unification works exactly as you would expect:
[X|Y] unifies with [a,b,c] via {X = a, Y = [b,c]}. [X|Y] unifies with [a,b,c,d] via {X = a, Y = [b,c,d]}. [X|Y] unifies with [a] via {X = a, Y = []}. [X|Y] does not unify with [].Now recall that a variable occurring in the head of a rule is treated universally, while a variable that occurs only in the body is handled existentially. Thus the first rule in the append definition
append([],List,List).
reads intuitively as: ``The result of appending the empty list [] to any list List is just List.'' A call to this rule will succeed as long as the first argument unifies with [], and the last two arguments unify with one another.Query Unifier Prolog answer ----------------------------------------------------------------- ?- append([],[b,c,d],[b,c,d]). {List = [b,c,d]} yes ?- append([],[b,c,d],X). {List = [b,c,d], X = [b,c,d]} X = [b,c,d] ?- append(X,Y,Z). {X = [], Y = List, Z = List} X = [], Y = Z ?- append([],[b,c],[b,c,d]). None noThe second call in the above table is normally the way we would use append, with the first two arguments instantiated, and the third a variable that will provide an answer.Now consider the second rule, which is the general case of appending a non-empty list to another list.
append([H|Tail],List,[H|NewTail]) :- append(Tail,List,NewTail).
All the variables that occur in this rule are universal variables since each occurs in the head of the rule. If we call append with the query:?- append([a,b,c],[d,e],Result).
The atom in the query does not unify with the first rule of append since the list [a,b,c] and [] do not match. The query however, unifies with the head of the second rule of append. According to unification, the resulting unifier is:{H=a, Tail=[b,c], List=[d,e], Result=[a|NewTail]}This substitution is applied to the body of the rule, generating the new query:?- append([b,c],[d,e],NewTail).
Thus by unifying the first argument of the query with the first parameter [H|Tail] in the head of the rule, we ``pull apart'' the list into its head and tail. The tail of the list then becomes the first argument in the recursive call.Let's examine what happens if we carry the trace all the way through. First, at the Prolog prompt you should enter `trace.', to start the trace facility. After starting tracing every query you enter will be traced. Just enter <return> when the interpreter hesitates. Enter the specified query (line 1 below) and enter return. The following is an annotated version of (approximately) what should appear on the screen.
1. ?- append([a,b,c],[d,e],Result). %% Initial call %% Result = [a|NewTail] 2. ?- append([b,c],[d,e],NewTail). %% First recursive call %% NewTail = [b|NewTail1] 3. ?- append([c],[d,e],NewTail1). %% Second recursive call %% NewTail1 = [c|NewTail2] 4. ?- append([],[d,e],NewTail2). %% Third recursive call exit 4 NewTail2 = [d,e] %% Unifying with base case %% of append. exit 3 NewTail1 = [c,d,e] %% Back substitution of %% NewTail2 exit 2 NewTail = [b,c,d,e] %% Back substitution of %% NewTail1 exit 1 Result = [a,b,c,d,e] %% Back substitution of %% NewTailIn the comments appearing on the right, we indicate the important substitutions to remember. In the first step, as the result of unifying the original query with the head of the second rule of append, the variable Result is unified with [a|NewTail] where NewTail is a variable that has yet to have a value (i.e. uninstantiated). In the second step where the first recursive call takes place, NewTail unifies with [b|NewTail1]. Note that each time a rule is used, the variables are considered to be new instances, unrelated to the variables in the previous call. This is the reason for the suffix 1 in the variable NewTail1, indicating that this is a different variable than NewTail.When computation reaches step 4, the first argument becomes the empty list []. This unifies with the first rule of append, and in the process the variable NewTail2 is unified with the list [d,e]. At this point, computation terminates and we ``unwind'' from the recursion. However, in the process of unwinding, we back substitute any variable that is instantiated in the recursion. That is how the final result of the append is constructed. Specifically, in unwinding from the recursive call in step 3, we back substitute the value of the variable NewTail2 inside [c|NewTail2]. The result is the list [c,d,e]. This list becomes the value stored in the variable NewTail1. Next to unwind from the recursive call in step 2, we back substitute the value of NewTail1 into [b|NewTail1]. Since from the previous step we just calculated NewTail1 to be the list [c,d,e], the current back substitution yields the list [b,c,d,e], which becomes the value stored for the variable NewTail. Finally, in the last unwind, the value of NewTail is back substituted inside [a|NewTail], producing the list [a,b,c,d,e]. This is now the final answer for the variable Result. The back substitution process just described illustrates how | acts as a list constructor that puts together an element with a list.
Example: Reversing a list
As another example, the following rules define a Prolog program for reversing lists. It works by recursion and makes use of append. A call to reverse requires two arguments, the first is the input list, and the second is the result of reversing.
reverse([],[]). %%% Reversing an empty list is the empty %%% list. reverse([H|Tail],Result) :- %%% Reverse a non-empty list, reverse(Tail,Tailreversed), %%% first reverse the tail, append(Tailreversed,[H],Result). %%% append the result %%% to list [H].Example: Membership
The following define rules to determine if something is a memeber of a given list:
member(X, [X|_]). member(X, [_|L]) :- member(X, L).
The symbol "_" in the above program, sometimes called "don't care", represents a generic variable; it could equivalently be replaced by any othe variable that does not already occur in the program.
Example: Selection Sort:
sel_sort([],[]). sel_sort(L,[Small|R]) :- smallest(L,Small) , delete(Small,L,Rest) , sel_sort(Rest,R) . /* smallest(List, Small) results in Small being */ /* the smallest element in List. */ smallest([Small],Small) . smallest([H|T],Small) :- smallest(T,Small) , Small=<H. smallest([H|T],H). /* delete(Elt,List,Result) has Result as List after deleting Elt. */ delete(Elt,[],[]) . delete(Elt,[Elt|T],T) . delete(Elt,[H|T],[H|NuTail]) :- delete(Elt,T,NuTail) .
- The Cut Symbol - Procedural Control:
Note: This section has been primarily copied from the Sicstus Prolog Manual.
Besides the sequencing of goals and clauses, Prolog provides one other very important facility for specifying control information. This is the cut symbol, written
!. It is inserted in the program just like a goal, but is not to be regarded as part of the logic of the program and should be ignored as far as the declarative semantics is concerned.The effect of the cut symbol is as follows. When first encountered as a goal, cut succeeds immediately. If backtracking should later return to the cut, the effect is to fail the parent goal, i.e. that goal which matched the head of the clause containing the cut, and caused the clause to be activated. In other words, the cut operation commits the system to all choices made since the parent goal was invoked, and causes other alternatives to be discarded. The goals thus rendered determinate are the parent goal itself, any goals occurring before the cut in the clause containing the cut, and any subgoals which were executed during the execution of those preceding goals.
For example:
member(X, [X|_]). member(X, [_|L]) :- member(X, L).
This predicate can be used to test whether a given term is in a list. E.g.
?- member(b, [a,b,c]).
returns the answer `yes'. The predicate can also be used to extract elements from a list, as in
?- member(X, [d,e,f]).
With backtracking this will successively return each element of the list. Now suppose that the first clause had been written instead:
member(X, [X|_]) :- !.
In this case, the above call would extract only the first element of the list (
d). On backtracking, the cut would immediately fail the whole predicate.x :- p, !, q. x :- r.
This is equivalent to
x := if p then q else r;
in an Algol-like language.
It should be noticed that a cut discards all the alternatives since the parent goal, even when the cut appears within a disjunction. This means that the normal method for eliminating a disjunction by defining an extra predicate cannot be applied to a disjunction containing a cut.
A proper use of the cut is usually a major difficulty for new Prolog programmers. The usual mistakes are to over-use cut, and to let cuts destroy the logic. A cut that doesn't destroy the logic is called a green cut; a cut that does is called a red cut. We would like to advise all users to follow these general rules.
- Write each clause as a self-contained logic rule which just defines the truth of goals which match its head. Then add cuts to remove any fruitless alternative computation paths that may tie up memory.
- Cuts are usually placed right after the head, sometimes preceded by simple tests.
- Cuts are hardly ever needed in the last clause of a predicate.
Example: Consider the Prolog program of our previous example:
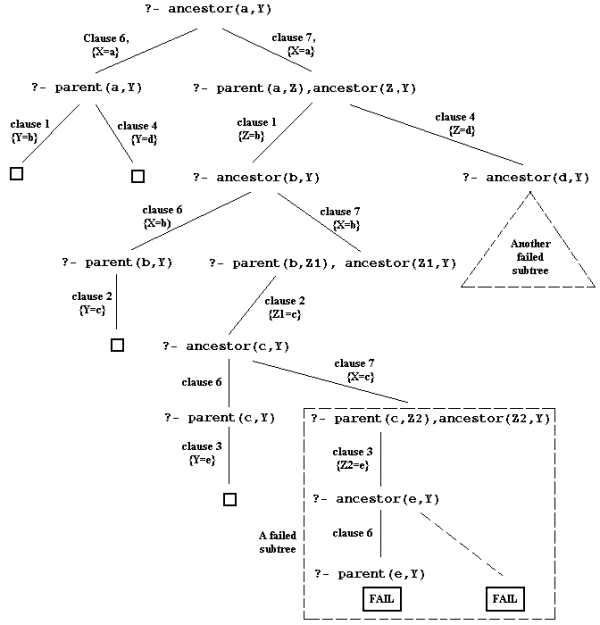
1. p(a, b). 2. p(a, c). 3. p(b, d). 4. p(c, e). 5. q(X, Y) :- p(X, Z), !, p(Z, Y).
Note that this time we have a cut ("!") inserted in the body of the last clause. Now given the same query as before (
?- q(a, W)), the effect of the cut will be to comit to the first choice of answer for W, i.e.,?- p(a, W). W = d; no
This is because upon backtracking, when the cut is reached again, it will cause the parent goal (
?- q(a, W)) to fail. Pictorially, we have the following computation tree:
- A Note of Interest
Resolution and unification appear in different guises in Computer Science and Mathematics.
- Resolution in logic programming:
(a \/ b) and (~b \/ c) gives (a \/ c)
- Elimination of variables in algebra:
a + b = 3 and -b + c = 5 gives a + c = 8.
- Procedure calls in programming:
procedure b(x) begin call a(x); end; ... call b(z); c; ...The above call to b(z) followed by the statement c will have the actual effect of:call a(z); c; ...
- Unification provides the mechanisms for parameter passing and access to record/structure components.
- Consequences of Logic's Procedural Interpretation
- Algorithm = Logic + Control
- We already have the logic component (specification)
- But, logic can also give us the control component (implementation)
- Specification = Implementation
- Programmer could simply write the specification and not have
to worry about procedural details of implementation.
- Program correctness is guaranteed (soundness).
- In practice, however, Prolog does have to introduce constructs for procedural control of programs, and has to worry about the order of computation.
- Lists in Prolog: