CSC 380/480 - Foundations of Artificial Intelligence - Winter 2007
Assignment 1
Due: Friday, Jan. 26
-
Consider the problem of designing a Web-based news filtering agent
which uses a static user profile (e.g., a set of keywords specified by
the user), and, on a regular basis, searches a specified news site
(e.g., Reuters or AP) for news stories that match the user profile. The
agent can search through the site by following links from page to page
(starting from the initial page). It then presents a set of links to
the matching stories that have not been read before. Matching is based
on the number of words from the profile occurring in the news story.
Give detailed answers to each of the following questions. Be sure to
state any assumptions you make about the capabilities and/or
limitations of the agent.
- Write a PEAS description of an agent for this environment.
- Characterize the environment as being observable, deterministic,
episodic, static, discrete, etc. (give a brief explanation for each).
- What agent architecture is best for this domain and why?
-
How would your answer to any of the above change, if we wanted the
agent to be able to dynamically obtain the user profile based on
passive observation of user's activity?
- Formulate the agent's task as a search problem (finding a news article
relevant to the user profile). Specifically, what would be the representation
for each state? What are the initial and goal states (in this representation)?
What is the successor function (how can one compute/generate the successors of a state)?
What is the cost function (how would path costs be computed)?
-
The Missionaries and Cannibals" problem: Three Missionaries and
three cannibals are on the left bank of a river. There is a boat on
their side of the river which can be used to carry one or two people.
The goal is to use this boat to cross the river in such a way that
cannibals never outnumber missionaries on either bank of the river.
Specify a state-space representation for this problem, including a
formal representation of each state, operators, the start state, and
the goal state. Draw the state-space graph for the problem (you only
need to include those states that are "legal," i.e., states in which
cannibals do not outnumber missionaries.
-
The four-peg version of the Towers-of-Hanoi puzzle is as follows. Four pegs – A, B, C, and D
– can each hold n rings at a time. There are n rings R1,
R2, …, Rn, such that Ri is
smaller than Rj for any i < j. A legal
placement of the rings on the pegs requires that (1) whenever any two rings
appear on the same peg, the smaller one is above the larger one and (2) all n
rings must be on pegs. In the start placement, all rings are on peg A. In the
goal placement, all rings are on peg D. The figure below shows the start state
for n = 4.
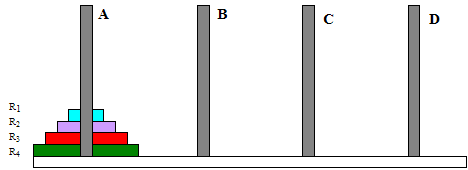
- Formulate this problem as a search problem, that is: (1) define a representation for each state; (2) give the
initial and goal states in this representation; and (3) define the successor function (describe how one can compute
the successors of a state).
- What is the total number of legal states?
- How many successors can a state
have at most?
-
The water-jug problem: You are given two jugs (one holds 4
gallons and the other 3 gallons of water). Assume that you are given no
external measuring device, that you can fill-up a jug from a pump any
time you need, and that you can pour water out of a jug or from one
into the other. The problem is to start from an initial state (each
state would be the status of the two jugs) and get to a final state by
a sequence of legal moves, e.g., from [0,0] (both jugs
are empty) to [2,0] (the 4-gallon jug has 2 gallons of
water and the three gallon jug is empty).
- Given the above state-space representation, specify (formally)
the operators for this problem as a set of production rules along with the
preconditions (used to reduce the search space). For example, each rule
can be expressed in the form:
(present state | preconditions) ==> (next state).
Some examples of such operators are:
- ([x, y] | x < 4) ==> [4, y] (i.e., fill the 4-galon jug);
- ([x, y] | x+y >= 4 and y > 0) ==> [4, y-(4-x)] (i.e., pour 3-gallon
jug into 4 gallon jug, until full);
- ([x, y] | x+y <= 4 and y > 0) ==> [x+y, 0] (i.e., pour all of the
3-gallon jug into the 4-gallon jug).
Your goal should be to have as few operators as possible to reduce the
complexity of the search space.
- Draw the full state-space graph for this problem.
- For the particular instance of the problem given above (going from
[0,0] to [2,0]), what would be a good
search strategy and why? Draw the search tree for this case based on your
proposed search strategy.
- Give the design of an agent that would solve the Water Jug problem.
Discuss your design decisions.
- Extra Credit: Implement the Water Jug agent based on your
design in the previous part of the problem.
Note: Extra Credit problems must be submitted separately from the assignment,
and by no later than March 11.
 Back to
Assignments Back to
Assignments
 Back to Main
Page Back to Main
Page
|

